What a Coincidence -- Unison Tuning
Music, whether it's seen or heard has three basic parts: rhythm, melody and harmony. Each of these
parts may be studied in great detail, but for this lesson let's simply define them as follows; rhythm is
time, melody is one sound at a time and harmony is two or more sounds at the same time. Now, what is
sound?
Non-musical sound is known by one name - Noise. However, musical sound is known by many names and the following are but a few; frequency, pitch, tone, letter and note. Let's look at this more closely.
Music we hear is sound and sound is "air moving". So what's moving the air? On the guitar, it's the strings that move the air. With your fingers or a pick, play any "open" string and watch it move back and forth. It's these back and forth vibrations that are moving the air. These vibrations can be counted and given a number. For now, we won't go into all that physics and acoustics stuff, like resonating bodies, air-pressure and amplitude.
The speed of the vibrations are steady, regular and predictable in time. And the number of times the string moves back and forth in one second is called Frequency. Frequency is measured in "cycles per second" (CPS) which is also known as Hertz (Hz), named after the 19th century German physicist Heinrich Hertz. The frequency range of the human ear is approximately 20 to 20,000 Hz and this may also be written as 20 Hz to 20 KHz. Kilo (K) is the Greek prefix for "thousand", 1Khz = 1000 Hz. So, how many times does a string move back and forth in one second? The answer depends upon which string is being played.
All six strings played either "open" or fretted vibrate faster than we can see and count, so science has to count for us - think electronic tuner. Not only are the vibrations counted and numbered, as we said earlier, but they may also be assigned a letter and note. For example: the "open" 5th string vibrates 110 times a second (110 Hz) and is called A, while the 2nd fret of the 3rd string vibrates an octave higher at twice the speed (220 Hz) and is also called A. And the 5th fret of the 1st string is also A, but it's frequency is two octaves higher (440 Hz). Remember, fast frequencies sound "high in pitch" and slow frequencies sound "low" - think Treble and Bass. It might help if we think about pitch as being either Absolute, Perfect or Relative.
By Absolute Pitch, I mean a specific frequency (definite pitch) assigned to a letter or note upon which everyone agrees. Did you know that the International Agreement which made A = 440 Hz the Absolute "Reference" Pitch used around the world today -- wasn't reached until 1939! Here are a few good sources of Absolute Pitch; a tuning fork, an electronic tuner, and a "tune-up pitch" from a play-along CD. Remember, cassette tapes are not a good source of Absolute Pitch due to the varying playback speeds of different tape players.
By Perfect Pitch, I mean "pitch memory". In other words, the ability to hear the Absolute Pitch and "perfectly" store it in your brain. Then later, without having to hear the Absolute Pitch again, locate and hear "inside your head" the frequency of that Absolute Pitch. In music school they call this "ear training" -- it takes a lot of practice!
Relative Pitch is the ability to hear the Absolute or Perfect pitch and then either match that pitch or locate another pitch relative to it. Tuning your guitar by matching or duplicating pitches is known as relative tuning or Unison Tuning.
In Latin, "uni" means one and "sonus" means sound, so unison means "one sound". However, unison is really a "co-incidence" - multiple events occurring at the same time. The prefix "co" means together (two or more as one) and an "incident" is an event. So unison really means "two tones of the same pitch sounding at the same time". One of the greatest things about the guitar is that you can play unison, by playing the same pitch on two or more strings. You can't do that on piano, woodwinds, brass or voice!
Now that we have an elementary understanding of the "science of sound", let's apply it to the tuning of the guitar. We'll begin by giving the six "open" strings their letter names and frequency numbers: 6th string E = 82.41 Hz, 5th string A = 110 Hz, 4th string D = 146.83 Hz, 3rd string G = 196 Hz, 2nd string B = 246.94 Hz and 1st string E = 329.62 Hz.
What follows is a method of Unison Tuning that will enable you to tune your guitar by ear! From an Absolute or Perfect source get an Absolute reference pitch. For example, if you want to tune the "open" 6th string, you'll need to hear an Absolute Pitch of E = 82.41 Hz. Next, assuming that the 6th string is in tune, play A = 110 Hz on the 6th string at the 5th fret. This pitch should match the "open" 5th string. If it does they're in unison and you're in tune. If they don't, you'll need to tune the 5th string higher or lower until they do sound the same. Be patient, this is relative tuning. The more you practice it -- the better you'll get.
When the 5th string is in tune, play D = 146.83 Hz on the 5th string at the 5th fret. This should match the "open" 4th string.
Then play G = 196 Hz on the 4th string at the 5th fret. This matches the "open" 3rd string.
Now to play B = 246.94 Hz on the 3rd string you must play at the 4th fret. This will match the "open" 2nd string. Don't forget this fret difference!
And finally, play E = 329.62 Hz on the 2nd string at the 5th fret. This will be in unison with the "open" 1st string.
Congratulations! You sound so much better -- now that you're in tune...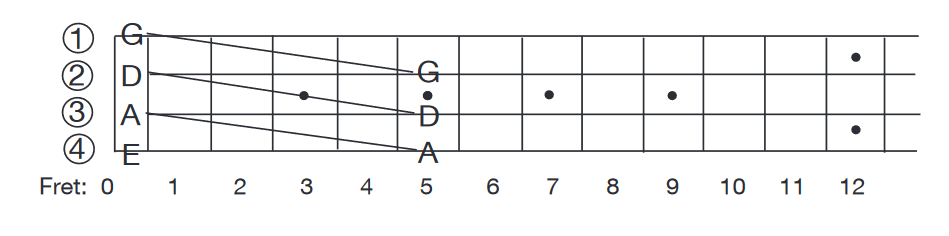
Non-musical sound is known by one name - Noise. However, musical sound is known by many names and the following are but a few; frequency, pitch, tone, letter and note. Let's look at this more closely.
Music we hear is sound and sound is "air moving". So what's moving the air? On the guitar, it's the strings that move the air. With your fingers or a pick, play any "open" string and watch it move back and forth. It's these back and forth vibrations that are moving the air. These vibrations can be counted and given a number. For now, we won't go into all that physics and acoustics stuff, like resonating bodies, air-pressure and amplitude.
The speed of the vibrations are steady, regular and predictable in time. And the number of times the string moves back and forth in one second is called Frequency. Frequency is measured in "cycles per second" (CPS) which is also known as Hertz (Hz), named after the 19th century German physicist Heinrich Hertz. The frequency range of the human ear is approximately 20 to 20,000 Hz and this may also be written as 20 Hz to 20 KHz. Kilo (K) is the Greek prefix for "thousand", 1Khz = 1000 Hz. So, how many times does a string move back and forth in one second? The answer depends upon which string is being played.
All six strings played either "open" or fretted vibrate faster than we can see and count, so science has to count for us - think electronic tuner. Not only are the vibrations counted and numbered, as we said earlier, but they may also be assigned a letter and note. For example: the "open" 5th string vibrates 110 times a second (110 Hz) and is called A, while the 2nd fret of the 3rd string vibrates an octave higher at twice the speed (220 Hz) and is also called A. And the 5th fret of the 1st string is also A, but it's frequency is two octaves higher (440 Hz). Remember, fast frequencies sound "high in pitch" and slow frequencies sound "low" - think Treble and Bass. It might help if we think about pitch as being either Absolute, Perfect or Relative.
By Absolute Pitch, I mean a specific frequency (definite pitch) assigned to a letter or note upon which everyone agrees. Did you know that the International Agreement which made A = 440 Hz the Absolute "Reference" Pitch used around the world today -- wasn't reached until 1939! Here are a few good sources of Absolute Pitch; a tuning fork, an electronic tuner, and a "tune-up pitch" from a play-along CD. Remember, cassette tapes are not a good source of Absolute Pitch due to the varying playback speeds of different tape players.
By Perfect Pitch, I mean "pitch memory". In other words, the ability to hear the Absolute Pitch and "perfectly" store it in your brain. Then later, without having to hear the Absolute Pitch again, locate and hear "inside your head" the frequency of that Absolute Pitch. In music school they call this "ear training" -- it takes a lot of practice!
Relative Pitch is the ability to hear the Absolute or Perfect pitch and then either match that pitch or locate another pitch relative to it. Tuning your guitar by matching or duplicating pitches is known as relative tuning or Unison Tuning.
In Latin, "uni" means one and "sonus" means sound, so unison means "one sound". However, unison is really a "co-incidence" - multiple events occurring at the same time. The prefix "co" means together (two or more as one) and an "incident" is an event. So unison really means "two tones of the same pitch sounding at the same time". One of the greatest things about the guitar is that you can play unison, by playing the same pitch on two or more strings. You can't do that on piano, woodwinds, brass or voice!
Now that we have an elementary understanding of the "science of sound", let's apply it to the tuning of the guitar. We'll begin by giving the six "open" strings their letter names and frequency numbers: 6th string E = 82.41 Hz, 5th string A = 110 Hz, 4th string D = 146.83 Hz, 3rd string G = 196 Hz, 2nd string B = 246.94 Hz and 1st string E = 329.62 Hz.
What follows is a method of Unison Tuning that will enable you to tune your guitar by ear! From an Absolute or Perfect source get an Absolute reference pitch. For example, if you want to tune the "open" 6th string, you'll need to hear an Absolute Pitch of E = 82.41 Hz. Next, assuming that the 6th string is in tune, play A = 110 Hz on the 6th string at the 5th fret. This pitch should match the "open" 5th string. If it does they're in unison and you're in tune. If they don't, you'll need to tune the 5th string higher or lower until they do sound the same. Be patient, this is relative tuning. The more you practice it -- the better you'll get.
When the 5th string is in tune, play D = 146.83 Hz on the 5th string at the 5th fret. This should match the "open" 4th string.
Then play G = 196 Hz on the 4th string at the 5th fret. This matches the "open" 3rd string.
Now to play B = 246.94 Hz on the 3rd string you must play at the 4th fret. This will match the "open" 2nd string. Don't forget this fret difference!
And finally, play E = 329.62 Hz on the 2nd string at the 5th fret. This will be in unison with the "open" 1st string.
Congratulations! You sound so much better -- now that you're in tune...

Return to Intermediate Lessons